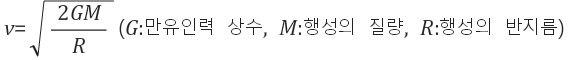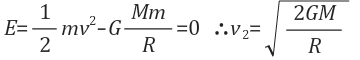행성의 탈출 속도

사는 이야기/과학사전

행성의 탈출 속도

후암동남산 2017. 1. 14. 11:35

행성의 탈출 속도

탈출 속도

▶ 탈출 속도

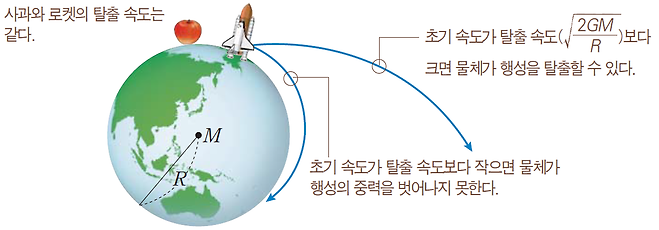
어떤 물체가 행성의 중력을 이기고, 그 행성을 벗어나기 위해 필요한 최소한의 초기 속도

탈출 속도의 크기 : 행성의 질량(M)이 클수록, 반지름(R)이 작을수록 탈출 속도가 크다.

물체의 질량과 탈출 : 속도 탈출 속도는 물체의 질량(m)과 관계없다. → 탈출 속도는 행성의 질량과 반지름만으로 결정되기 때문

탈출 속도의 의미 : 행성의 탈출 속도가 클수록 물체가 행성을 탈출하기 어렵다.

행성과의 거리와 탈출 속도 : 행성의 표면에서 멀어질수록 중력의 크기가 감소하므로 탈출 속도는 작아진다.

행성의 탈출 속도는 행성의 질량(M)이 클수록, 행성의 반지름(R)이 작을수록 큰 값을 갖는다.
탈출 속도는 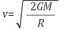과 같으므로 반지름이 지구의 2배이고 질량은 8배인 행성은 탈출 속도가 지구의 2배가 된다.

행성의 탈출 속도

지구형 행성은 탈출 속도가 작고, 목성형 행성은 탈출 속도가 크다. → 행성의 이 클수록 탈출 속도가 크기 때문

▶ 천체 표면에서의 탈출 속도

구분	지구형 행성				목성형 행성				태양
구분	수성	금성	지구	화성	목성	토성	천왕성	해왕성	태양
질량(지구=1)	0.05	0.82	1.00	0.11	318	95.2	14.5	17.1	330,000
반지름(지구=1)	0.38	0.96	1.00	0.53	11.2	9.45	4.01	3.89	109
탈출 속도 (km/s)	4.3	10.4	11.2	5	60	36	21	24	617.7

행성의 대기와 탈출 속도

탈출 속도가 작은 행성일수록 기체가 행성을 쉽게 탈출해 대기를 갖기 어렵고, 탈출 속도가 큰 행성일수록 기체가 행성을 탈출하기 어려워 더 많은 대기를 포함할 수 있다.

달과 수성은 탈출 속도가 작아서 기체 분자가 쉽게 벗어나 대기가 거의 없다.

▶ 행성의 탈출 속도 유도하기

행성 표면에서의 역학적 에너지(E)는 다음 식으로 나타낼 수 있다.

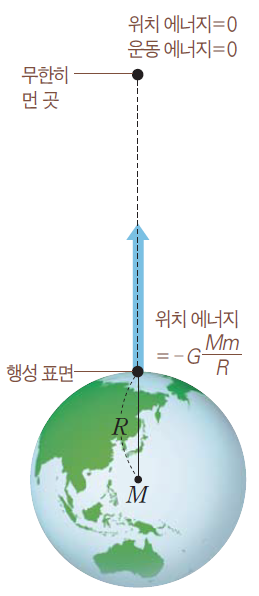
행성에서 무한히 먼 지점에서의 역학적 에너지는 0이다.
- 운동 에너지=0 → 쏘아 올린 물체가 행성을 벗어나 무한히 먼 곳에 도달하면 멈추게 되어 속도가 0이 되므로 운동 에너지는 0이 된다.
- 위치 에너지=0 → 행성에서 무한히 멀어지면 위치 에너지가 0이 된다.
- 역학적 에너지=운동 에너지+위치 에너지=0+0=0

탈출 속도(ve) : 물체를 무한히 먼 곳으로 보내려면, 에너지 보존 법칙에 의해 행성 표면에서의 역학적 에너지가 0이 되게 물체를 쏘아 올려야 한다. 이때의 속도가 탈출 속도이다.

- 물체의 초기 속도가 탈출 속도보다 작을 때(E<0) → 물체는 행성을 벗어날 수 없다.
- 물체의 초기 속도가 탈출 속도보다 클 때(E>0) → 물체는 행성을 탈출한다.
→ 행성의 중력을 벗어나기 위해 필요한 최소한의 초기 속도가 탈출 속도이다.

티스토리