피보나치 수열에 대하여 다음 등식이 성립하는 것을
수학적 귀납법을 사용하여 증명하시오.
1. 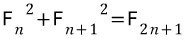
2. 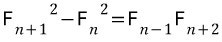
3. 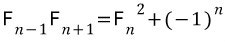
피보나치 수열을 F(1) = F(2) = 1, n >= 1 일때 F(n+2) = F(n+1)+F(n) 인 것으로 보겠습니다.
사실 F(1) = 0 으로 하거나 시작을 0 으로 해도 같은 결과가 나옵니다.
m, n >= 1 일때 F(n+m+1) = F(n+1)F(m+1) + F(n)F(m) 인 것을 보입니다.
strong induction 으로 증명합니다.
n = 1 일때 F(2)F(k+1) + F(1)F(k) = F(k+1) + F(k) = F(k+2) = F(1+k+1) 성립합니다.
1 <= k <= n 인 모든 k에 대해서 F(n+m+1) = F(n+1)F(m+1) + F(n)F(m) 가 성립한다고 가정하면,
n+1 일때,
F(n+1+m+1) = F(n+m+1) + F(n+m) = F(n+m+1) + F((n-1)+m+1) =
{ F(n+1)F(m+1) + F(n)F(m) } + { F((n-1)+1)F(m+1) + F(n-1)F(m) } = (n일때의 가정 사용)
F(n+1)F(m+1) + F(n)F(m) + F(n)F(m+1) + F(n-1)F(m) =
F(m+1)*(F(n+1)+F(n)) + F(m)*(F(n) + F(n-1)) =
F(n+2)F(m+1) + F(n+1)F(m) =
F((n+1)+1)F(m+1) + F(n+1)F(m)
수학적 귀납법에 의해 성립합니다.
이제 m = n 을 넣으면,
F(n+n+1) = F(n+1)F(n+1) + F(n)F(n)
따라서 F(2n+1) = F(n+1)^2 + F(n)^2
2.
여기서는 일단 n >= 2 여야 문제가 성립합니다.
F(n+1)^2 - F(n)^2 =
{ F(n+1) + F(n) } * { F(n+1) - F(n) } =
F(n+2)*{ F(n-1) + F(n) - F(n) } =
F(n+2)F(n-1)
3.
n >= 2 일때 라고 해야 문제가 성립되겠습니다.
n = 2 일때 F(1)F(3) = 2, F(2)^2 + (-1)^2 = 2 성립합니다.
n >= 2 일때 F(n-1)F(n+1) = F(n)^2 + (-1)^n 이 성립한다고 하면,
(뒤에서 F(n)^2 = F(n-1)F(n+1) - (-1)^n 을 써먹겠습니다)
n+1 일때,
F(n+1-1)F(n+1+1) = F(n)F(n+2) =
F(n)*(F(n) + F(n+1)) = F(n)^2 + F(n)F(n+1) =
F(n-1)F(n+1) - (-1)^n + F(n)F(n+1) =
F(n+1)*(F(n-1)+F(n)) + (-1)^(n+1) =
F(n+1)*F(n+1) + (-1)^(n+1) =
F(n+1)^2 + (-1)^(n+1)
수학적 귀납법에 의해 성립합니다.
'사는 이야기 > 수학사전' 카테고리의 다른 글
| 기약분수와 유한소수와의 관계... (0) | 2013.01.08 |
|---|---|
| 근과 계수와의 관계 (0) | 2012.12.29 |
| 피보나치 수열 (0) | 2012.12.23 |
| [수학공부법] 수학 공부하는 패턴을 바꿔야 성적이 오른다 (0) | 2012.12.17 |
| 산술기하평균 코시 슈바르츠 부등식 (0) | 2012.12.05 |