등차수열
등차수열(arithmetic sequence, 等差數列)은 연속하는 두 수의 차이가 일정한 수열을 뜻한다. 예를 들어 1, 3, 5, 7, 9, ...은 등차수열이다. 이때 두 수의 차이를 공차(common difference)라고 한다. 예를 들어, 앞의 수열의 공차는 2이다.
수열의 첫항을  , 공차를
, 공차를  라고 하면 등차수열의 n번째 항은 다음과 같이 나타낼 수 있다.
라고 하면 등차수열의 n번째 항은 다음과 같이 나타낼 수 있다.
등차수열 구하기[편집]
등차수열의 항과 공차 이용[편집]
 번째 항을
번째 항을  , 공차를
, 공차를  라 하면 등차수열의 일반항은 다음과 같다.
라 하면 등차수열의 일반항은 다음과 같다.
물론 여기에 i=1을 대입하면 잘 알려진 일반항으로 다음을 얻는다.
이를테면 제5번째 항이 9이고, 공차가 2라면
from nucha68@naver.com
공차[편집]
등차수열에서 연속하는 두 수의 차이를 공차(公差)라고 한다. 보통  로 표시한다.
로 표시한다.
예시를 들면 다음과 같다.
- 1, 2, 3, 4,…으로 증가하는 수열이 있을 때, 공차
 는 1이다.
는 1이다. - 2, 10, 18, 26, …으로 증가하는 수열이 있을 때, 공차
 는 8이다.
는 8이다. - 1, 1, 1, 1, 1, … 이런 수열이 있을 때, 공차
 는 0이다.
는 0이다. - 342, 345, 348,351 …으로 증가하는 수열이 있을 때, 공차
 는 3이다.
는 3이다. - 23461234, 23843963, 24226692, 24609421, …으로 증가하는 수열이 있을 때 공차
 는 382729이다.
는 382729이다. - 0, -1, -2, -3, -4 …으로 증가하는 수열이 있을 때, 공차
 는 -1이다.
는 -1이다.
등차중항[편집]
세 수  ,
,  ,
,  가 이 순서로 등차수열을 이룰때,
가 이 순서로 등차수열을 이룰때,  를
를  와
와  의 등차중항이라고 한다. 세 수
의 등차중항이라고 한다. 세 수  ,
,  ,
,  에 대하여
에 대하여  가
가  와
와  의 등차중항이면 등차수열의 정의에 의해서
의 등차중항이면 등차수열의 정의에 의해서  이므로 다음이 성립한다.
이므로 다음이 성립한다.
등차중항은 등분점이라고 생각하면 쉽다. 세 수  ,
,  ,
,  가 이 순서로 등차수열을 이룰때,
가 이 순서로 등차수열을 이룰때,  는
는  와
와  의 이등분점이다. 네 수
의 이등분점이다. 네 수  ,
,  ,
, 
 가 이 순서로 등차수열을 이룰때,
가 이 순서로 등차수열을 이룰때,  는
는  와
와  의 1:2 내분점이고
의 1:2 내분점이고  는
는  와
와  의 2:1 내분점이다. 즉,
의 2:1 내분점이다. 즉,  와
와  는 삼등분점이 된다.
는 삼등분점이 된다.
수열의 정의상 함수처럼 생각하면 이를 내분점, 혹은 외분점의 의미로 받아 들일 수 있다. 항의 비로 표현이 가능하다. [1]
합 구하기[편집]
초항부터 n번째 항까지의 합  는 다음과 같은 공식으로 나타난다.
는 다음과 같은 공식으로 나타난다.
이것은 다음과 같은 방법으로 증명할 수 있다.
결론적으로 등차수열의 합의 원리는 { }의 평균값 x {
}의 평균값 x { }의 항의 개수로 정리 할 수 있다.(단, {
}의 항의 개수로 정리 할 수 있다.(단, { }은 유한수열)
}은 유한수열)
등차수열의 합의 원리는 실생활에서는 도형의 넓이(ex-사다리꼴의 넓이)를 구하는데 주로 사용된다.
또 다른 방법[편집]
사람들은 다음과 같은 형태의 합을 쉽게 계산할 수 있다.
S = -5-4-3-2-1+0+1+2+3+4+5
S = 0임을 쉽게 알 수 있다.
등차수열의 합도 이와같은 방법을 이용할 수 있다.
즉 양끝의 합이 0이 되도록 양끝의 합의 평균을 구해 항의 갯수만큼 빼주는 것이다.
그 평균값을 m이라 하면
Sn = a1 + a2 + a3 + ... + an-2+an-1+an
양변 m을 n개 빼주면 우변은 위와 같은 형태로 쉽게 0이 되어버린다.
Sn - m * n = 0
Sn = m * n
Sn = (a1 + an)/2 * n
Sn = n(a1+an)/2
'사는 이야기 > 수학사전' 카테고리의 다른 글
| 선형미분 방정식에서 역연산자를 이용하여 특수해 y를 구하는 방법 (0) | 2013.11.15 |
|---|---|
| 기회비용 (0) | 2013.09.29 |
| 고교수학 공식 모음집 (0) | 2013.09.06 |
| 중앙값 (0) | 2013.09.05 |
| 표본평균의 표준편차의 의미 (0) | 2013.08.31 |

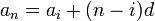



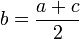
![S_n = \frac{n(a_1 + a_n)}{2} = \frac{n[2a_1 + (n-1)d]}{2}](http://upload.wikimedia.org/math/1/3/4/134fa4927dc3bef1cd63f89449590a13.png)
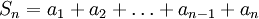
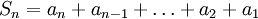

![2S_n = [2a_1 + (n-1)d] + [2a_1 + (n-1)d] + \dots + [2a_1 + (n-1)d] + [2a_1 + (n-1)d]](http://upload.wikimedia.org/math/c/b/6/cb680ff89875c62271daf683ed9dad47.png)
![2S_n = n[2a_1 + (n-1)d]](http://upload.wikimedia.org/math/9/d/4/9d4a206cb27163f01c4910edb6990beb.png)
![S_n = \frac{n[2a_1 + (n-1)d]}{2}](http://upload.wikimedia.org/math/5/f/a/5fa9bda213b9fc59d0c53a8b8f32f315.png)