프랙탈

프랙탈

목차

 

1. 프랙탈 기하학
2. 폰 코흐의 곡선
3. 만델브로트 집합
4. 줄리아 집합
5. 프랙탈 차원

수학자들의 관점에서 보면 프랙탈은 복잡한 기하학적 형태이다. 프랙탈의 핵심 개념은 자체 유사성이다. 자체 유사성을 가지고 있는 물체는 부분을 이루는 요소들이 전체와 닮은 형태를 하고 있다. 이는 양치식물의 잎에서 쉽게 발견할 수 있다. 잎을 자세히 살펴보면 아주 작은 부분도 전체와 비슷한 모양을 하고 있다. 놀랍게도 이런 형태는 미세한 크기까지 계속된다.

양치식물의 잎에서 프랙탈 구조를 관찰할 수 있다.

잎의 형태에서 보여지는 유사성을 발견하기까지는 오랜 시간이 걸렸다. 그럼에도 아직 발견하지 못한 여러 가지 형태들이 자연에는 존재하고 있다. 우리는 구름을 늘 관찰해왔다. 그러나 구름이 얼마나 큰지 또는 작은지 이야기할 수 있는 사람이 있을까? 멀리 있는 구름은 크고 가까이 있는 구름은 작다고 할 수 있을까?

구름은 거리와 관계없이 같은 모양으로 보인다. 구름은 아주 클 수도 있고, 반대로 아주 작을 수도 있지만 그 모양은 비슷하다. 크기에 관계없이 같은 모양을 하고 있는 이러한 성질을 통계적 자기 유사성이라고 한다. 가장 흥미로운 독립적 형태는 산맥, 나무 그리고 심지어는 우주의 물질 분포에서도 발견할 수 있다.

프랙탈 기하학

프랙탈은 비유클리드적 불규칙 형태를 기술하는데 매우 유용해 프랙탈의 개념을 프랙탈 기하학이라고 부르는 새로운 기하학 체계가 나타났다. 수학의 범주를 벗어나 물리화학이나 유체역학과 같은 복잡한 세상으로 들어간 것이다.

프랙탈 기하학이 은하단의 형성을 설명하는데 응용되었다.

(이 사진은 우리은하 안에 있는 구상성단의 사진으로, 은하단의 사진이 아님.)

프랙탈 기하학이 응용되는 가장 흥미로운 분야 중 하나는 통계역학이다. 또한 우주에 흩어져 있는 은하단의 분포와 같은 카오스적 행동 체계에 프랙탈 기하학이 잘 들어맞는다는 것이 증명되었다.

폰 코흐의 곡선

폰 코흐의 곡선은 정삼각형을 반복적으로 만들 때 형성되는 비교적 단순한 프랙탈 구조이다. 처음에는 하나의 정삼각형을 다른 삼각형 위에 뒤집어 놓는다. 계속해서 외부의 변들을 3등분한 후 각 변의 중심 부분을 이용해 새로운 정삼각형을 만든다. 이러한 과정을 프랙탈 구조가 나타날 때까지 반복한다.

처음 네 번째까지의 코흐 곡선

코흐 곡선을 이용하여 만든 눈송이 형태

만델브로트 집합

‘프랙탈’이라는 단어는 1975년 폴란드 태생의 수학자 베노이트 만델브로트(Benoit Mandelbrot)가 처음 사용했다(이 단어는 조각이라는 뜻을 가진 라틴어 fractus에서 유래했다). 만델브로트는 만델브로트 집합이라고 부르는 가장 유명한 프랙탈 구조를 제안했다. 이 프랙탈은 순수한 수학적 세계에만 존재하는 아름다운 형태로, 컴퓨터의 도움을 받아 직접 눈으로 볼 수 있다.

만델브로트 집합은 다음 방정식을 반복적으로 계산하면 얻어진다.

z=z²+c

이 방정식은 사람의 눈을 현혹시킬 수 있을 만큼 간단한 형태이지만 z와 c가 복소수라는 점이 특징이다. 컴퓨터를 이용하여 만든 다음의 만델브로트 집합의 영상은 이 방정식을 반복적으로 사용해 얻어진 값들을 다른 색깔로 나타내 만들었다.

현대 컴퓨터가 없었다면 이것은 불가능했다. 그러나 프랙탈 알고리즘이 없었다면 현대 컴퓨터라도 만델브로트 집합을 만들어내지 못했을 것이다. 프랙탈 알고리즘은 프랙탈 기하학을 발전시켜 자연의 복잡하고 불규칙한 형태를 컴퓨터 화면에 재현시킬 수 있도록 한다.

컴퓨터로 만든 만델브로트 집합

만델브로트 집합을 꼼꼼하게 살펴보면 자기 유사성의 법칙을 확인할 수 있을 것이다. 또한 얼음판의 갈라진 틈들과 겨울날 창문 위에 만들어지는 서리의 형태에서 발견할 수 있는 자연의 카오스적 형태를 여기서 찾아볼 수 있을 것이다.

줄리아 집합

줄리아 집합[개스턴 줄리아(Gaston Julia)의 이름을 딴]은 복소수 평면에서 정의된 프랙탈 구조이다. 줄리아 집합은 만델브로트 집합과 밀접한 관계가 있으며, 줄리아 집합도 반복적인 계산 결과를 다른 색깔로 나타내 만든다.

프랙탈 차원

프랙탈의 기본 특징은 –복잡한 비유클리드적 형태를 이해하는데 필수적인- 프랙탈 차원이다. 프랙탈 세계에서의 차원은 유클리드 기하학의 차원과는 다르다. 프랙탈 차원은 형태를 확대하거나 또는 아주 작은 규모에서 보더라도 항상 같은 값을 가진다. 코흐의 프랙탈 곡선을 자세히 살펴보면 각 단계마다 곡선을 이루는 직선의 길이가 3분의 1로 줄어들고, 직선의 개수는 4배 증가해 총 길이가 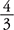씩 증가한다는 것을 알 수 있다. 프랙탈 차원을 D라고 하면 길이는 3분의 1로 줄어들면서 개수가 4배 증가하는 코흐 곡선의 경우 차원(D)은 다음과 같은 방정식을 이용해 나타낼 수 있다.

3^D=4