삼각방정식 삼각부등식

(8) 삼각방정식 삼각부등식 

 

삼각방정식과 삼각부등식을 하기 전에 방정식을 함수로, 부등식도 함수로 해석할 수 있어야 합니다.

부등식이건 방정식이건 함수로 해석하는 방법은 그래프로 해석을 하자는 뜻이거든요.

좌변과 우변에 'y='을 붙여서 두 개의 함수식으로 만든 다음 두 개의 함수의 그래프를 그려서 교점을 찾으면 됩니다.

 

예를 들어, x²-4x+3=0이라는 방정식이 있을 때, 실근의 x값을 구하라고 한다면

인수분해해서 (x-3)(x-1)=0이라고 두고

(x-3)이랑 (x-1)랑 곱해서 0이 됐으므로 (x-3)이 0이 된던가 또는 (x-1)이 0이되어야 하기 때문에

x=3 또는 x=1이라고 하는게 방정식의 풀이입니다.

 

아무튼 x²-4x+3 = 0를 함수로 해석하면 양 변에 y=을 붙여서 가운데 있는 등호를 교점이라고 생각하면 됩니다. 

 x²-4x+3=0의 양 변에 각각 y=을 붙이면

y=x²-4x+3

y=0 (x축)

이 두개의 함수식이 나오는데 이 두개의 함수의 그래프의 교점을 구하면 되는겁니다.

y=x²-4x+3의 x절편은 얼마인가요? x절편이란 y가 0일 때의 x값이므로 y가 0이라면 x값은 3과 1이 나옵니다.

 

그 이차함수의 그래프와 x축을 그려보면

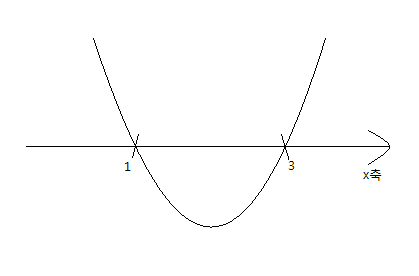
결국, x=1과 x=3이 '실근'이 되는건데..

함수로 해석하면 '교점의 x좌표'라고 하는 겁니다.

 

여기서 정리하고 넘어가야하는게

실근을 구하라는 소리는 교점을 구하라는 소리나 마찬가지라는 겁니다.

실근이 없다라는 소리는 두 그래프의 교점이 없다라는 것이며

실근이 하나이다라는 소리는 두 그래프의 교점이 하나라는 소리입니다.

 

예전에 많이 봤음직한 문제인데요.

임의의 x값에 대하여 ax²+bx+c≠0일 조건을 구하라고 했을 때, 함수로 해석하자면

y=ax²+bx+c, y=0이 ≠로 연결되어있으니까, 두 그래프가 서로 교점을 가지지 마라! 두 그래프가 서로 만나지 마라! 이런 뜻이거든요.

즉, 교점이 없다는 이야기는, 실근이 없다는 이야기고, 허근이 나와야한다는 소리입니다!!

 

따라서 ax²+bx+c≠0일 조건을 구하면 판별식(D)<0라고 푸시면 됩니다.

 

 

 

 

이것처럼!

삼각방정식이란 각자리에 미지수가 들어간 방정식을 말하는데

삼각방정식도 이것과 똑같습니다.

 

위의 삼각방정식을 풀라고 했을 때, 어떤 이는 그냥 "sin30도가 ½이니까 x는 30˚요, 그러니까 에요."라고 말하는 사람이 있는데

 

그렇지 않습니다. 틀렸습니다! 30˚만 맞을까요? 답은 또있어요. 답은 무수히 많아요.

그 이유는 함수로 해석하면 알아요.

y=sinx와 y=의 그래프를 동시에 그려봤는데 교점은 몇개인가요?

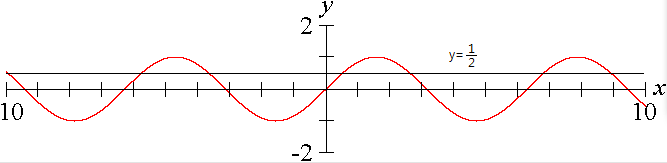
답은 무수히 많습니다. 싸인은 한없이 구부러지는 그래프잖아요?

 

 그래서 밤위란것이 항상 주어지게 되어있습니다.

아래처럼요

 

 

그렇다면 y=sinx와 y=½의 교점 중에서 0과 2π사이에 있는 교점만 찾으면 됩니다.

두 개의 교점이 보이죠? 그런데 싸인이나 코싸인은 0~90˚(0~π/2)와 90˚~180˚(π/2~π)끼리 서로 대칭이랍니다.

그래서 하나의 점이 30도라면 아래와 같이 표현이 가능합니다.

따라서 하나의 교점의 x좌표가 (30˚)라면 하나의 교점의 x좌표는 π(180˚)에서 (30˚)를 뺀 것이므로

 

 

 

의 실근은

라고 구해주시면 됩니다.

 

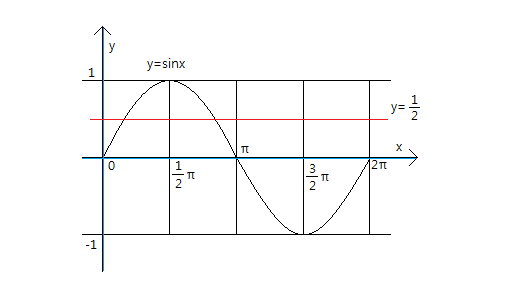
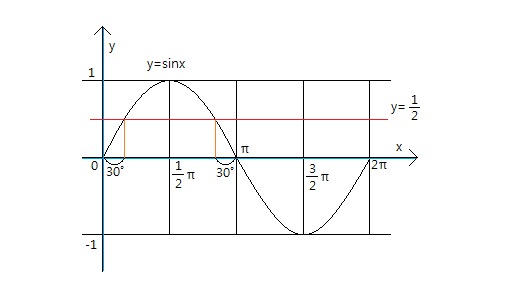
무슨 말인지 알겠죠?

 

그런데 만약 문제가

 를 만족하는 실근의 합을 구하라고 한다면

라고 구해놓고 두 근을 구해서 π라고 답을 쓸 수도 있지만

굳이 이렇게 안풀어어도 됩니다.

 

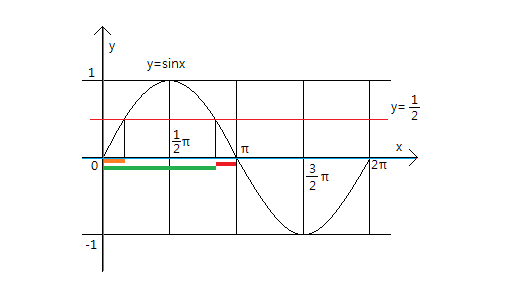
아래와 같이 교점이 2개이므로 실근도 2개가 나오는데..

아래의 그림에서 보면 하나의 근이 '왼쪽 주황색선'의 길이라면 다른 하나의 근은 '초록색선'의 길이인데

왼쪽의 주황색 선은 오른쪽의 빨간선의 길이와 같으므로 결국 실근의 합은 초록색길이+빨간색길이이므로 π가 답이 됩니다.

 

 

만약

의 실근을 모두 더하라고 문제가 나와도 풀 수 있겠죠?

똑같이 그림을 그려서 길이의 대칭을 이용해서 합을 한꺼번에 구하는겁니다.

비록 각각의 실근은 구할 수 없지만, 실근의 합은 구할 수 있거든요..

 

 

 

 

 

 

예제 1

2cos²x+7sinx-5=0 (0≤x≤2π)의 해를 모두 구하면?

 

[풀이]

sin²x+cos²x=1이므로

cos²x=1-sin²x

따라서 원래의 식을 2(1-sin²x)+7sinx-5=0으로 바꿀 수 있다.

정리하면 2sin²x-7sinx+3=0이 된다.

sinx를 치환하자.

sinx=t (-1≤t≤1) → 싸인의 범위때문에 t의 범위가 만들어짐

2t² - 7t + 3 = 0

인수분해하면 (2t-1)(t-3)=0

따라서 t=½ 또는 t=3

그러나 -1≤t≤1라는 범위가 있으므로

t는 3이 되지 못하므로, t=½

t=sinx이므로

결국

sinx=½ (0≤x≤2π)←처음에 주어진 x의 범위

인데 아까 풀어본 문제이니까

그래프는 그렸다고 치고

결국 답은 

 

 

 

이제 부등식을 할거거든요?

부등식도 마찬가지에요.

함수로만 해석한다음 크다, 작다를 위에있다, 아래있다라고 생각해주시면 됩니다.

sinx > cosx (0≤x≤2π) 라는 문제가 있다면 양변에 y=을 붙여서

y=sinx > y=cosx (0≤x≤2π)

이라고 보고 두 그래프를 그린 후, y=sinx의 그래프가 더 위에있는 범위를 찾아주시면 끝납니다!

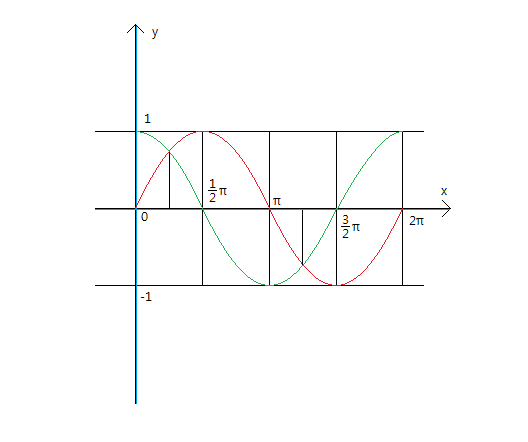
두 그래프의 교점의 x좌표는 얼마일까요?

다른 말로 sinx = cosx 는 어떤게 있나요?

특수각 중에서 45˚는 싸인값과 코싸인값이 같죠..

 

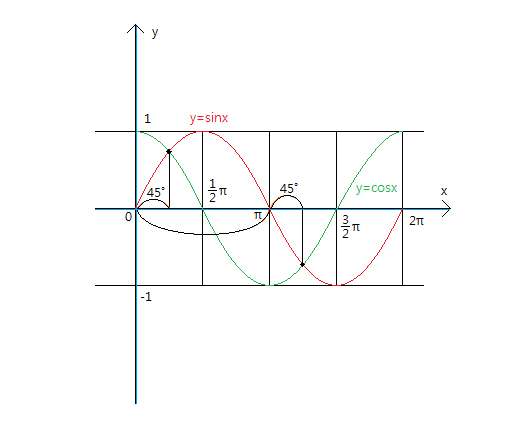
즉, 위에 보이는 교점중에서 90˚이내에 생기는 교점의 x좌표는 45˚가 되고

위에 보시다 싶이 또 하나의 교점의 x좌표는180˚에서 45˚만큼 더하면 되니까 225˚가 됩니다.

 

따라서 y=sinx > y=cosx (0≤x≤2π)를 해석해서

sinx가 cosx보다 위에있는 x의 범위를 찾으면

45˚< x < 225˚

라는 값이 나옵니다.

라디안으로 쓰면

 

 

 

 

 

아래의 문제도 풀어볼까요.

2cos²x - 3sinx ＜ 0 (0≤x≤2π)

 

[풀이]

sin²x+cos²x=1이므로

cos²=1-sin²x

따라서 원래의 식은 2(1-sin²x) - 3sinx ＜ 0가 된다.

정리하면 2sin²x + 3sinx -2  ＞ 0

sinx를 t로 치환하자.

sinx=t ( -1≤t≤1 )

2t² + 3t -2 > 0

인수분해하면

(2t-1)(t+2) > 0

부등식을 풀면

t<-2 또는 t>½ 인데 ( -1≤t≤1 )이므로

t>½인데 t=sinx이므로

sinx > ½의 값만 찾아주면 된다.

양 변에 y=을 붙여서 그래프를 그리면

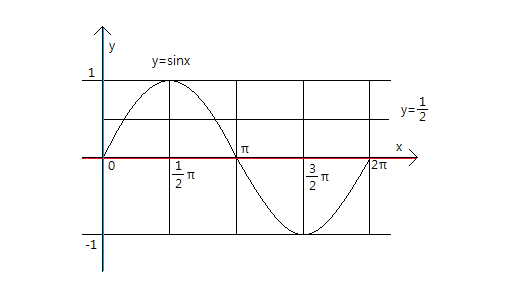
인데 sinx > ½이므로 y=sinx가 y=½보다 위에있는 범위를 찾으면

 

가 답이 된다.

 

 

 

 

 

또 한 문제만 풀어볼까요?

 

sin2x=½ (0≤x≤2π) 의 실근의 개수를 구하라고 한다면 한번 직접 그려보세요.

sin2x의 그래프는 0≤x≤2π의 범위에서 sinx보다 2배 빠르게 그리잖아요?

y=sinx와 y=½의 교점은 2개인데 y=sin2x은 sinx가 2개 있는것과 비슷하므로 y=½와의 교점은 4개가 됩니다.

따라서 답은 4개인데

 

sin2014x=½ (0≤x≤2π)의 실근의 개수는 몇 개가 될까요?

2028이 됩니다. 0≤x≤2π의 범위에서 sinx의 형태의 그래프가 2014개가 빼곡히 그려지는데 주기 1개당 2개의 교점을 가지므로

4028개의 교점을 가지게 되는 것 이랍니다.

[출처] 제12장 삼각함수 - (8) 삼각방정식 삼각부등식 |작성자 SperoSpera