삼각함수의 정의
직각삼각형에서 직각이아닌 한 각이 주어지고, 아무 한 변의 길이만 알면 삼각비(sin, cos, tan)를 이용하여
다른 두 변의 길이를 표현할 수 있습니다.
< 빗변이 주어졌을 때 >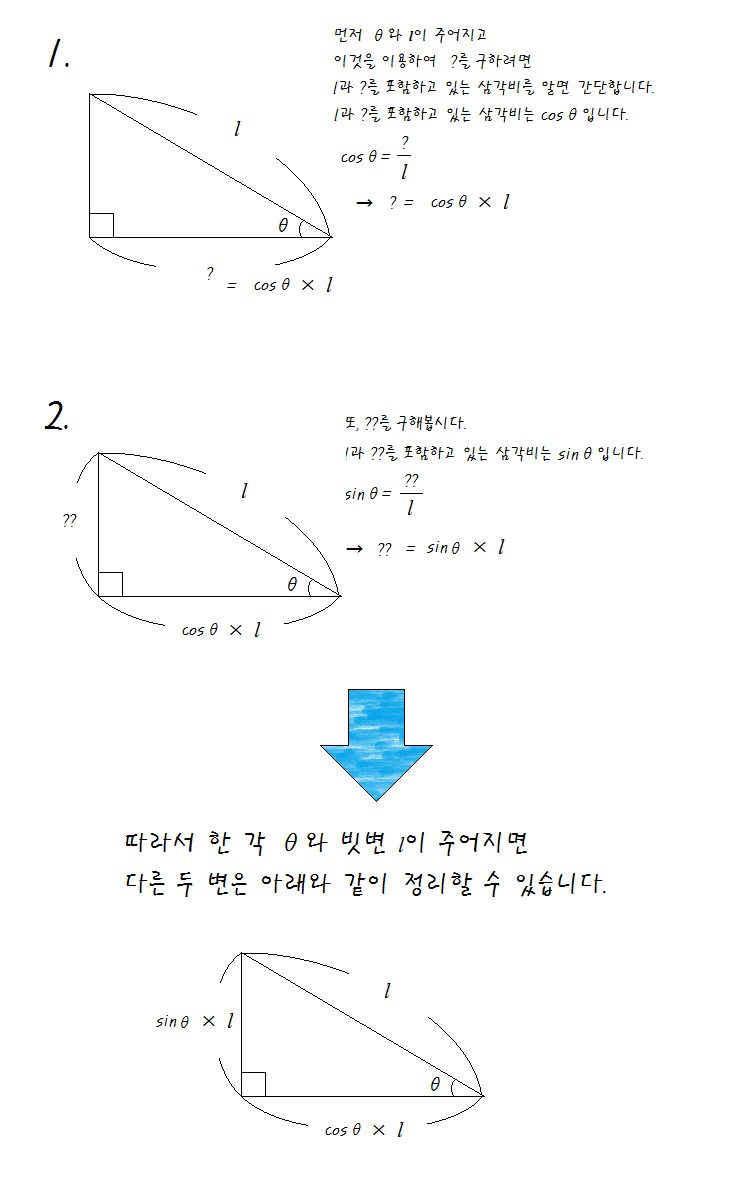
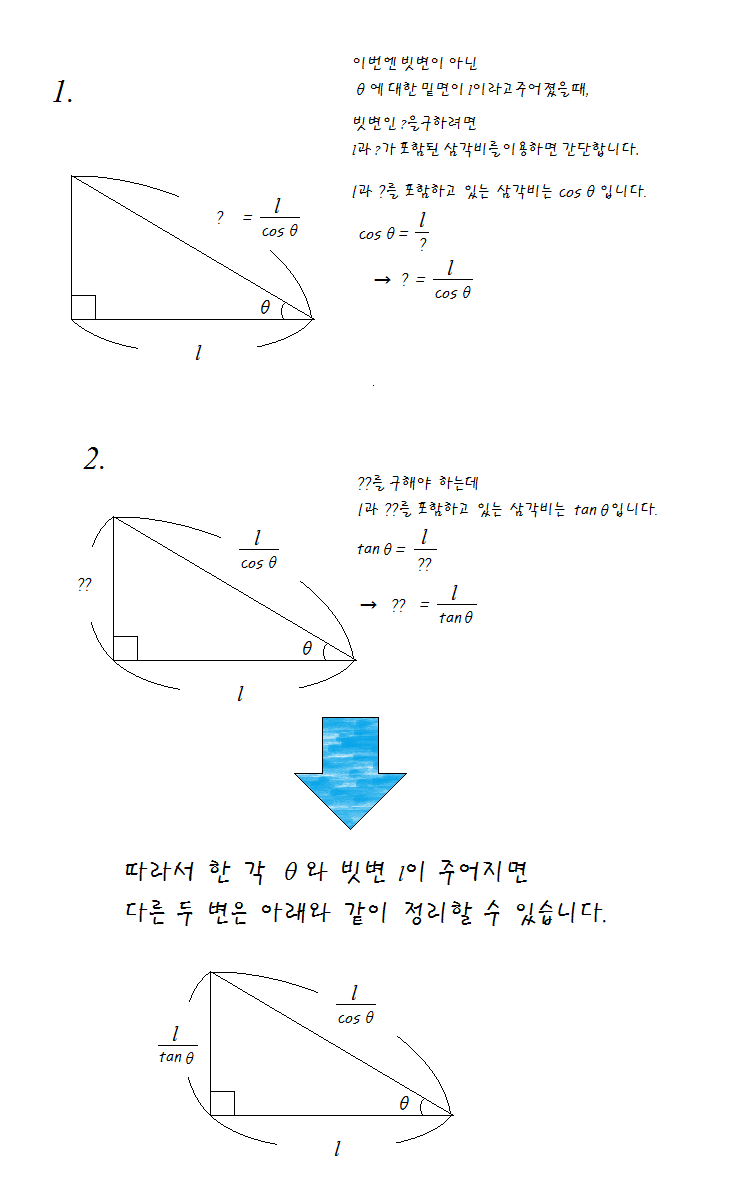
< 빗변이 아닌 변이 주어졌을 때 >
이해하기 쉽도록설명은 이렇게 했지만 필자는 이런식으로 바꾸지 않습니다. 너무 오래걸리기 때문이죠.
제가 구하는 방법과 비슷하게나마 설명을 해드리면
일단 주어진 각에서 주어진 하나의 변과 구하고자 하는 변을 포함하는 삼각비를 찾습니다.
먼저 주어진 변이 빗변이라면 구하고자 하는 변은 주어진변과 두 변을 포함하는 삼각비를 곱해주면 됩니다.
주어진 변이 빗변이 아니라면 구하고자 하는 변은 두 변을 포함하고 있는 삼각비 분의 주어진 변이 됩니다.
뭐.. 바꿀 수 있다는게 중요하고, 방법이 중요한것은 아니니 넘어가겠습니다.
이제
이것을 이용해 빗변이 1인 직각삼각형이 주어졌을 때, 나머지 두 변의 길이를 표현하면 아래와 같습니다.
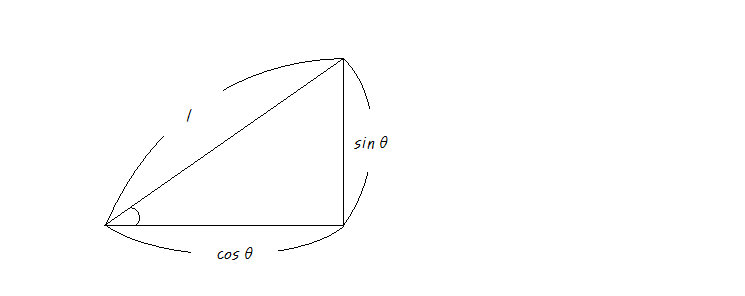
그런데 피타고라스의 정리를 이용하면
![]() 이라는 아주 거룩한 공식이 나오게 됩니다.
이라는 아주 거룩한 공식이 나오게 됩니다.
또, 이 삼각형을 아래와 같이 밑면을 x축에 포개고 각을 원점에 붙여서 좌표평면에 대응시키면
오른쪽 위의 꼭지점의 좌표가 ( cosθ , sinθ )인 점으로 바꿔서 표현이 가능함을 느낄 수 있을겁니다.
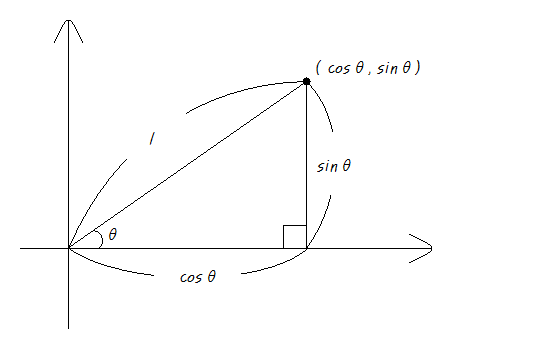
여기서 sin함수와 cos함수의 정의가 만들어집니다.
여태까지는 직각삼각형을 통해서 sin과 cos을 삼각비라는 이름으로 정의했잖아요?
그렇지만 그 정의는 안타깝게도 직각삼각형의 내부의 각은 90도를 넘기지 못하기 때문에 90˚를 넘기는 sin과 cos값을 구할 수 없습니다.
그러나 방금 좌표평면에 표현한 cos함수와 sin함수의 방법으로는
90˚가 넘는 120˚나 210˚의 삼각함수 값을 정의할 수 있게 됩니다.
아래와 같이 말입니다.
일단 살펴보시면 대충 무슨소린지 알 수 있을 겁니다.
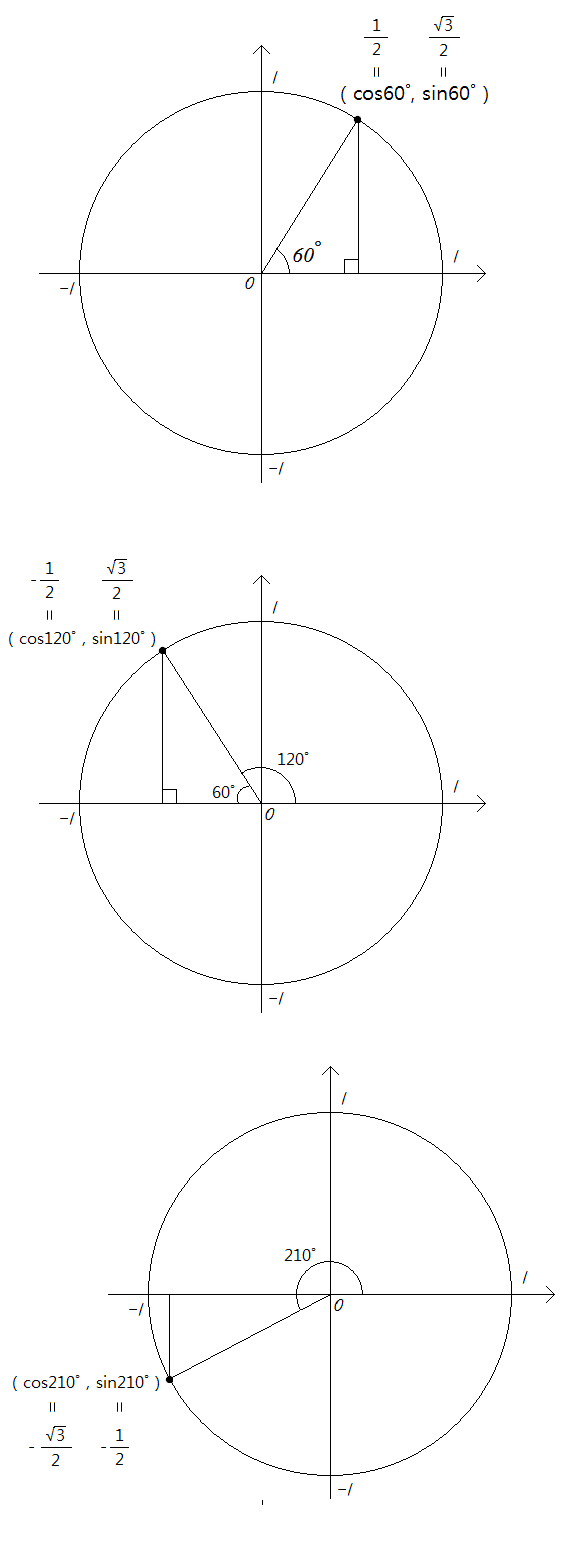
일반화 하자면 아래와 같이 표현이 가능하지요.
결국엔 반지름이 1인 단위원에서 원을 지나는 한 점을 잡으면
직각삼각형의 원리에 의해 그 점의 x좌표를 cosθ, y좌표를 sinθ라고 할 수 있다는 겁니다.
<반지름이 1인 원을 단위원이라고 합니다.>
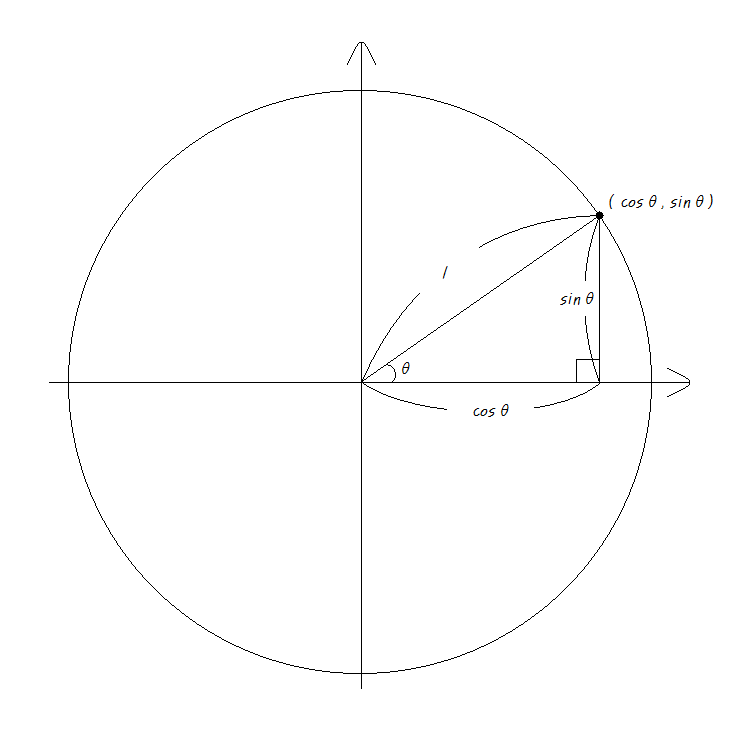
이것은 극좌표랑 비슷한 건데요. 모르면 그냥 알아둡시다.
음.. 위에서 삼각함수를 정의할 때, 쓰인 규칙이라고 보시면 됩니다.
각을 나타낼 때..
양수를 가지는 x축을 시초선이라고 부릅니다. 즉, 위의 그림에서 1사분면과 4사분면 사이에 있는 기준선이 시초선입니다.
그리고 위의 삼각형에서는 빗변이 보이죠?
빗변으로 볼 수도 있지만 시초선에서 θ라는 각을 나타내게 하는 반직선이라고 생각하셔도 됩니다. 이것을 "동경"이라고 합니다.
또, 원점을 중심으로 반시계의 방향을 양의 방향, 시계의 방향을 음의 방향이라고 정의한답니다..(아래그림 참조!!)
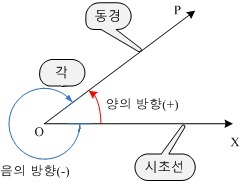 그림 참조 : http://blog.naver.com/jklee517/150172134680
그림 참조 : http://blog.naver.com/jklee517/150172134680
어쨌든 이 삼각함수의 정의는 결국 무슨소리냐면 아까 적었듯
반지름이 1인 원(단위원)을 만든 다음에 θ의 각도를 나타내는 동경과 원과 만나는 점을 찍으면
그 점의 x좌표는 cosθ, y좌표는 sinθ라고 놓으면 θ라는 각도가 90˚를 벗어나더라도,
sin과 cos의 값을 구할 수 있다는 이야깁니다.
아래의 예를 통해서 부연설명을 하도록 하겠습니다.
ⓐ 60˚
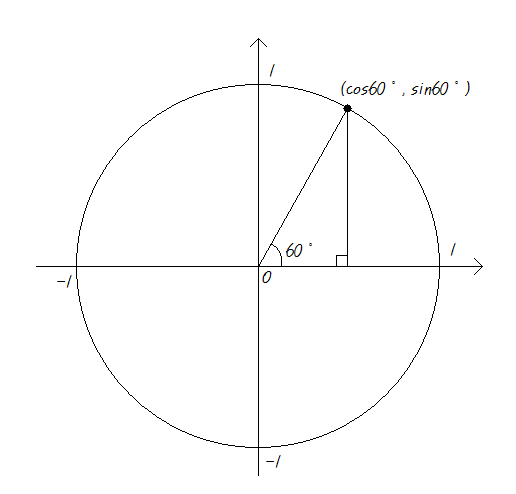
이것은
시초선에서 양의 방향으로 60˚만큼 동경을 그어 중심이 원점인 단위원과 만나게 하면
만나는 점의 x좌표는 cos60˚, y좌표는 sin60˚라는 이야기랍니다.
ⓑ 120˚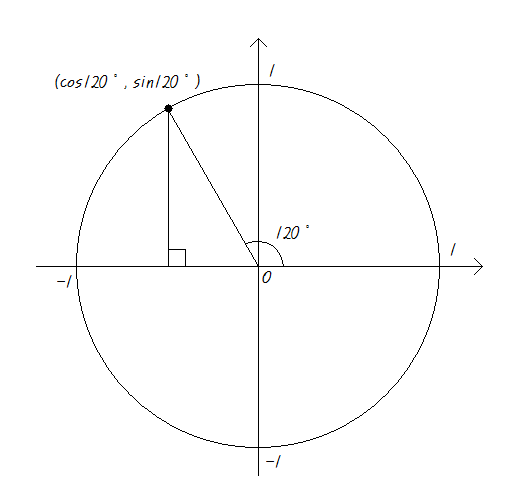
이것도 마찬가지로
양의 방향으로 120˚의 동경과 원점이 중심인 단위원과 만나는 지점은 120˚의 sin값과 cos값을 구할 수 있다는 소리입니다.
물론 정확한 값은 모르겠지만 cos120˚가 양수가 아닌것만은 보이죠?
x축만 놓고 보세요. cos120˚는 원점보다 왼쪽에 있으므로 음수가 맞습니다.
그리고 다시한번 말하지만 이것이 sin과 cos의 정의입니다.
tan는 cos분의 sin이므로 각각 구해준 다음에 분수로 만들면 됩니다.
역시 결국은 말하고 싶은건
단위원과 θ의 동경과의 교점의 x좌표를 cosθ, y좌표를 sinθ라고 읽자. 이게 끝입니다.
그리고, cos의 정의는 무엇이냐. 단위원과의 교점에서 x좌표라고 하면 되고, sin의 정의는 단위원과의 교점에서의 y좌표라고 생각하시면 됩니다!!
뭐 이것을 이용해 어떤 문제를 풀자는 것은 아니지만
정의는 확실히 익히고 가시는게 나중에 도움이 되기 때문이죠.
....
그럼 cos180˚를 구해보세요.
180˚를 나타내는 동경을 그린 후에, 단위원과의 교점에서 x좌표를 구하면 되죠?
아래와 같이 답은 -1이 되죠.
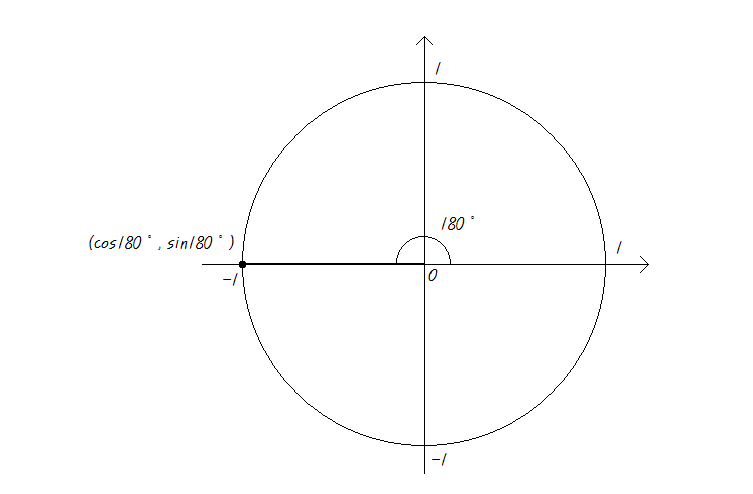
그렇다면
각 사분면의 각도의 범위..이것도 아시나요?
좌표평면은 x, y축을 기준으로 4가지 부분으로 나누어집니다. 그것을 시초선 위에 부분부터 반시계방향으로 각각 1사분면부터 4사분면으로 정의합니다.
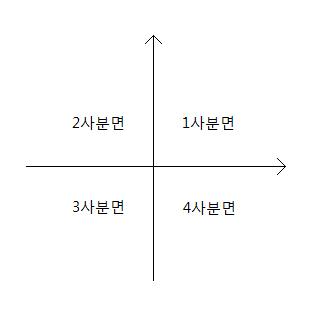
1사분면은 0˚~90˚
2사분면은 90˚~180˚
3사분면은 180˚~270˚
4사분면은 270˚~360˚
로 나누어집니다. (0˚, 90˚, 180˚, 270˚, 360˚는 경계면에 있어서 어느 사분면에도 포함되지 않습니다.)
그냥 0에서 90씩 더하면 경계점이 됩니다.
그런데 맞춰보세요. sin130˚는 음수일까요, 양수일까요?
sin130˚는 단위원에서 130˚의 동경과의 교점에서 y좌표입니다. 음수입니까 양수입니까?
머리속으로 그려보세요.
단위원과 130˚의 동경과의 교점을 머리속으로 그려보고.. 그 교점의 y좌표가 0윗쪽에 존재합니까 아랫쪽에 존재합니까?
윗쪽에 존재하죠? 즉, 양수입니다.
다음문제 cos 250˚도 맞줘보세요.
마음속으로 다시한번 그려보세요. 250˚는 3사분면에 있어요..
3사분면에 존재하는 각에서 원과의 교점의 x좌표는 음수인가요 양수인가요?
음수랍니다.
사실.. y좌표는 sin이고 x자표는 cos이라는 사실만 기억하고 각이 몇사분면에 속하는지만 금방 구할 수 있으면
쉽게 풀 수 있습니다. 참고로 tan는 sin과 cos의 분수관계이므로, 싸인과 코싸인이 부호가 같으면 tan는 양수가 되고, 부호가 다르면 음수가 됩니다.
1사분면은 x, y좌표가 모두 양수만 오니까 cos, sin모두 양수이고 덕분에 tan도 양수
2사분면은 x좌표가 음수, y좌표가 양수이므로 cos은 음수, sin은 양수, 그러므로 tan는 음수
3사분면은 x, y 좌표 모두 음수가 되니까 cos, sin 모두 음수. 결국 tan는 양수
4사분면은 x좌표는 양수, y좌표는 음수이므로 cos은 양수, sin은 음수, 그러므로 tan는 음수
이것을 그냥 암기할 수도 있는데
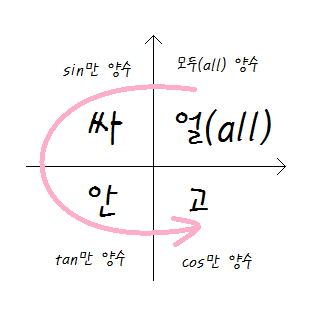
1사분면의 각이라면 모두(all)양수
2사분면의 각이라면 sin만 양수 (나머지는 음수)
3사분면의 각이라면 tan만 양수 (나머진 음수)
4사분면의 각이라면 cos만 양수 (나머지음수)
1,2,3,4순서대로 양수인것만 얼싸안고(all, sin, tan, cos)라고 외우기도 합니다.
정리
1. 삼각비의 정의 : 원점이 중심인 단위원과 θ의 동경과의 교점의 x좌표를 cosθ, y좌표를 sinθ

→ sinθ의 정의 = 단위원과 θ의 동경과의 교점에서 y좌표
cosθ의 정의 = 단위원과 θ의 동경과의 교점에서 x좌표
2.
![]()
3.

[출처] 제12장 삼각함수 - (3) 삼각함수의 정의|작성자 SperoSpera
'사는 이야기 > 수학사전' 카테고리의 다른 글
| 삼각비의 정의 (0) | 2015.01.26 |
|---|---|
| 라디안(호도법) : 각의 표현 (0) | 2015.01.26 |
| 각바꾸기 공식 (0) | 2015.01.26 |
| 삼각함수의 제곱관계식과 반지름이 r일 때의 정의 (0) | 2015.01.26 |
| 삼각함수의 그래프 Ⅱ (0) | 2015.01.26 |