명제
1. 명제의 의미
명제란 객관적으로 참과 거짓을 구분할 수 있는 문장으로 추상적이고 주관적인 견해를 철저히 배재한 문장입니다.
예를 들어,
〔 이 사과는 맛이있다. 그녀는 이쁘다. 그 사람은 생김새가 멋있다. 〕
이 세 문장들은 사람에 따라 참과 거짓이 갈리는 추상적이고 주관적인 문장입니다.
따라서 이러한 문장은 명제가 아닌 문장입니다.
저 문장을 굳이 명제로 바꾼다면
〔 이 사과의 당도는 15.6브릭스로 평균보다 높다. 그녀는 5000명의 남자의 설문조사 결과 90%의 선호도로 집계됐다. 〕
이 정도가 될 것이죠..
다만 주의해야 할 것은 명백히 거짓인 문장 또한 명제라는 사실입니다.
명제의 뜻이 참과 거짓을 구별할 수 있는 문장이니까. 참이든 거짓이던 명제라는 것이죠. (명제=참인 명제+거짓인 명제)
2. 조건
"사람이다." 라는 문장은 참일까요 거짓일까요.
질문을 바꿔보지요.
"x는 자연수다."라는 문장은 참인가요 거짓인가요?
답은 참도 아니고 거짓도 아닙니다.
왜냐하면 이 문장은 명제가 아니라 그냥 조건문이기 때문입니다. x에 따라 참과 거짓이 달라지기 때문이죠.
그런데 이 조건문을 참이되게 하는 x의 집합을 진리집합이라고 합니다.
그리고 알파벳으로 조건문과 진리집합을 표시할 때,
조건은 알파벳 소문자 p, q, r 순으로 많이 쓰고 그의 진리집합을 각각의 영어 대문자를 사용해 P, Q, R 순으로 많이 쓰는게 관례입니다.
예를 들어, "조건문 p: x는 자연수이다."라고 할 때, 조건문 p를 참이되게 하는 진리집합 P는 {1, 2, 3, 4, ..}가 되겠죠.
3. 명제의 표현
조건문 p와 q에 관해 'p이면 q이다'를 화살표로 p→q라고 표현합니다.
예를 들어, 조건 p, q에 관하여
p: x는 자연수
q: x는 양수
를 만족한다면 q→p는 "양수이면 자연수이다."라는 뜻이 되고, p→q는 "자연수이면 양수이다."라는 문장이 됩니다.
p→q가 참인 명제이므로 참인 명제는 특별히 p⇒q라고 표현합니다.
또, 명제 p,q와 그의 진리집합 P, Q에 관하여, p⇒q라면 P⊂Q가 항상 성립하게 됩니다.
예를 들어,
p가 4의 배수, q가 짝수라고 한다면
p의 진리집합 P는 {4, 8, 12, 16, 20, ···· }
Q의 진리집합 Q는 {2, 4, 6, 8 , 10, ···· }인데
p⇒q이므로 P⊂Q가 항상 성립합니다.
4. 명제의 부정
먼저 명제를 부정하는 법을 배워야 합니다.
"대한민국의 남자는 군대에 간다."을 한번 부정해보도록 할것인데요.
일단 먼저 한번 이 명제의 참과 거짓을 구별해보겠습니다.
대한민국 남자인데도 군대에 안가는 사람이 존재하죠? 그러므로 위 문장은 거짓입니다. (참고로 명제에 반하는 예가 하나라도 있다면 그 명제는 거짓입니다.)
그리고 "대한민국의 남자는 군대에 간다."를 부정해 보겠습니다.
어떤 사람은 단어 한자 한자를 다 부정하려고 합니다.
대한민국의 반대는 북한, 남자의 반대는 여자! 군대의 반대는 사회! 간다의 반대는 왔다.
따라서 "대한민국의 남자는 군대에 간다."의 :부정은 북한 여자는 사회에 온다"??
(X)
당연히 아니겠죠.
부정은 단어 하나 하나의 부정이 아닌
그 문장의 전체 의미의 부정입니다.
결론부터 말하자면 동사와 몇몇 관사를 부정하는 것입니다.
'--한다'의 부정 : '--하지 않는다.'
'모든'의 부정 : '몇몇'
집합에서 여집합을 배웠죠? 그 집합을 제외한 나머지.. 부정도 똑같은 비슷한 개념입니다.
'모든 자연수는 양수이다.'를 부정하면 '몇몇의 자연수는 양수가 아니다'가 되지요.
그렇다면
"대한민국의 남자는 군대에 간다."는 대한민국 남자이면 군대에 간다이므로
"모든 대한민국 남자 → 군대에 감"입니다.
이것을 부정하면 "몇몇의 대한민국의 남자는 군대에 가지 않는다."가 되지요.
그런데 왜 '모든'의 부정이 '어떤'일까요?
어떤 명제의 부정명제란 반댓말의 개념이 아니라 그 명제가 거짓이 되게하는 명제를 의미하는 것입니다.
예를 들어, "모든 사람은 군대에 간다"가 거짓이 되려면 적어도 1사람만 군대에 가지 않아도 모든 사람이 군대에 가는 것은 거짓이 됩니다.
그러므로 적어도 1사람을 "어떤"이라는 말로 표현해서 "어떤 사람은 군대에 가지 않는다"가 부정이 되는겁니다.
반대로 '어떤'을 부정하면 '모든'이 됩니다.
예를 들면, "어떤 사람은 1000살이 되어도 죽지 않는다."의 부정은 모든 사람이 1000살 이전에 죽는다는 것을 보이면 되기 때문입니다.
즉, 모든 사람이 1000살 이전에 죽는다는 것은 한사람도 1000살이상동안 사는 사람이 없다는 것이죠.
부정한다는 것은 ~라는 기호로 약속이 되어있습니다. 예를 들어, 조건 p의 부정은 ~p라고 씁니다.
※ 기타 수식의 부정
<의 부정은 ≥
≤의 부정은 >
=의 부정은 ≠
'또는'의 부정 '그리고'
'그리고'의 부정 '또는'
예를 들어, 조건 p, q가 아래와 같다.
p:a, b는 짝수이다.
q:a+b는 짝수이다.
p→q는 'a, b가 짝수라면 a+b는 짝수이다.'
p→q의 부정은 ~p → ~q이므로 'a, b가 짝수가 아니라면, a+b는 짝수가 아니다.'가 된다.
주의
ⓐ 조건 p가 a=b=c라면 이 조건의 부정 ~p는 a≠b 또는 b≠c (또는 c≠a)가 된다.
왜냐하면 a=b=c는 a=b 그리고, b=c라는 의미이기 때문이다.
ⓑ 조건 q가 a<b<c라면 이 조건의 부정 ~q는 a≥b 또는 b≥c이다.
왜냐하면 a<b<c이라는 소리는 a<b 그리고 b<c라는 소리이기 때문이다.
5. 명제의 역, 이, 대우
명제가 p→q라면
역이란 q→p을 뜻하고
이는 ~p→~q를 뜻하고
대우는 ~q→~p를 뜻합니다.
ⓐ 명제가 참이라면 명제의 대우도 참이고, 명제가 거짓이라면 명제의 대우도 항상 거짓이다.
ⓑ 명제의 대우가 참이라면 그 명제도 참이고, 그 대우가 거짓이라면 명제도 거짓이다.
ⓒ 명제의 역이 참이라면 명제의 이 또한 참이되고, 그 역이 거짓이라면 이 또한 거짓이다.
( 이것을 진리값이 서로 일치한다라고 한다. ) → 명제와 대우 // 역과 이는 서로 진리값이 일치한다.
ⓓ 어떤 명제가 참이어도 그 명제의 역과 이는 거짓일 수도 있고 참일 수도 있다.
( 명제의 참/거짓과 역과 이의 참/거짓은 관련이 없다. )
6. 충분조건과 필요조건
충분조건과 필요조건은 조건과 조건사이의 포함관계를 나타내주는 것이라고 보시면 됩니다.
예를 들어, p라는 조건이 'x는 대한민국 사람(국적이 한국인 사람)이다.'이고 q라는 조건이 'x는 서울시민이다.'라고 하죠.
만약 어떤 사람이 서울시민이라면 그 사람은 분명 일단 대한민국사람이라는 것이 전제여야 합니다.
즉, 반드시 한국 국적을 먼저 취득해야 서울시민이 될 자격이 먼저 생긴다고 할 수 있는것이죠.
따라서 한국사람은 서울시민이기 위하여 반드시 필요한 조건이라고 하여 필요조건이라고 합니다.
또, 만약 어떤 사람이 이미 서울시민이라면 그 사람은 이미 대한민국 사람의 자격이 선취득했을 것이므로
서울시민이라면 이미 한국 국적을 얻기위한 자격은 이미 충분하다고 하여 충분조건이라고 합니다.
즉, 한국사람은 서울시민이기 위한 필요조건이고, 서울시민은 한국사람이 되기위한 충분조건이라고 합니다.
이것을 벤다이어그램으로 보면 충분조건과 필요조건이 무엇인지 좀 더 확실한 설명이 되겠지요.
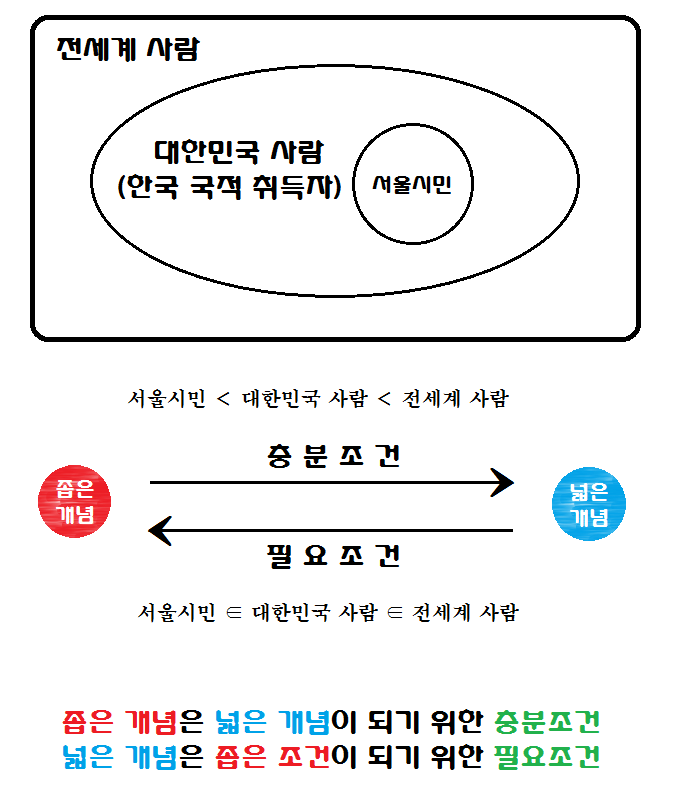
필요충분이라는 것도 있는데요.
이것은 두개의 조건이 완전히 일치할 때, 두 조건 사이의 관계를 '필요충분조건'이라고 합니다.
예를 들어, 1+2는 3이기 위한 필요충분이라고 하죠.
이번엔 중요한 명제로 설명해보겠습니다.
조건 p, q가 p ⇒ q라는 명제를 만족할 때, 앞의 조건 p는 (q이기 위한) 충분조건이며, 뒤의 조건 q는 (p이기 위한) 필요조건이라고 합니다.
또한, 원래의 명제인 p ⇒ q와 그의 역인 q ⇒ p가 모두 참이면 p와 q사이의 조건을 필요충분조건이라고 하지요.
예를 들어,
아까처럼 조건p가 x는 대한민국 국민, 조건q가 x는 서울시민이라고 할 때,
p→q①와 q→p②라는 명제를 만들면
①대한민국 국민이면 서울시민이다.
②서울시민이면 대한민국 국민이다.
①은 거짓인 명제가 되고
②는 참인 명제가 되므로
1번과 2번 중
q ⇒ p 이 2번만 만족하게 되지요.
이것은 서울시민 ⇒ 대한민국 국민
...이므로 서울시민은 대한민국 국민이기 위한 충분조건이고, 대한민국 국민은 서울시민이기 위한 필요조건이라고 합니다.
결론은 명제의 참은 '작은 범위 → 큰범위'가 성립하므로
작은범위는 큰 범위가 되기위한 충분조건이고, 큰 범위는 작은 범위의 필요조건이라는 것입니다.
[출처] 제1장 집합과 명제 I - (2) 명제|작성자 SperoSpera
'사는 이야기 > 수학사전' 카테고리의 다른 글
| 집합 (0) | 2015.01.26 |
|---|---|
| 집합의 용어 (0) | 2015.01.26 |
| 정수부터 복소수까지의 확장 (0) | 2015.01.26 |
| 곱셈공식과 이중근호 (0) | 2015.01.26 |
| 루트를 이용한 간접조건 (0) | 2015.01.26 |