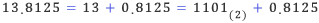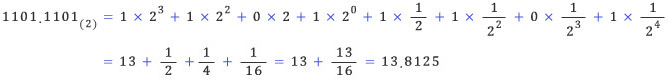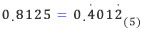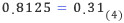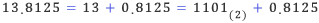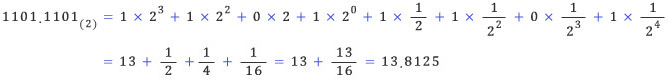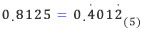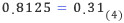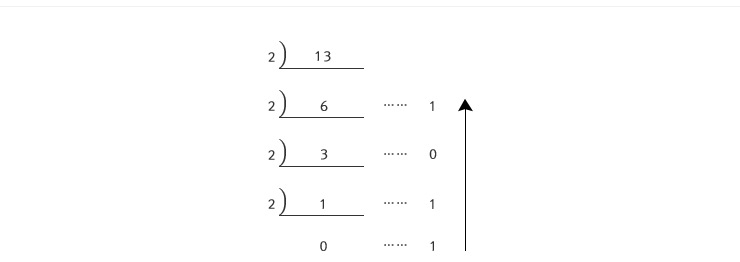
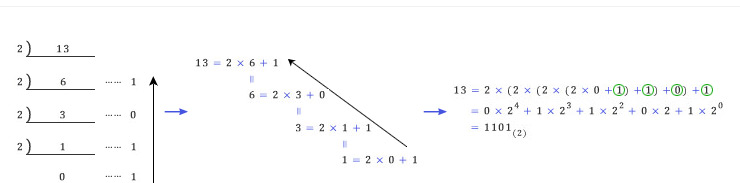
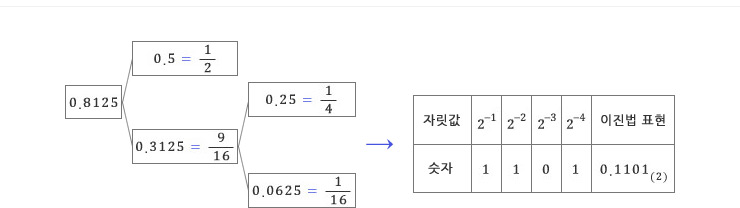
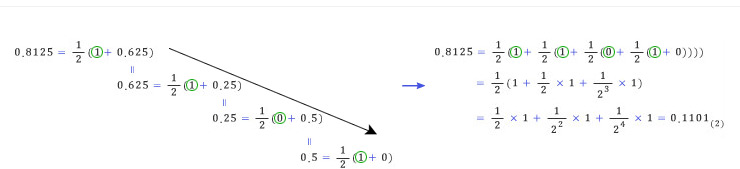
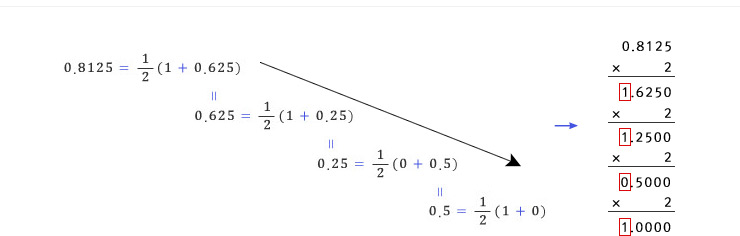
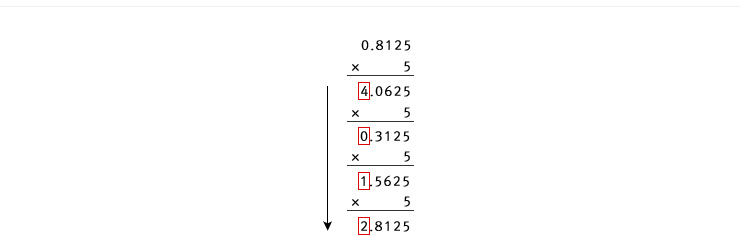
소수의 진법전환

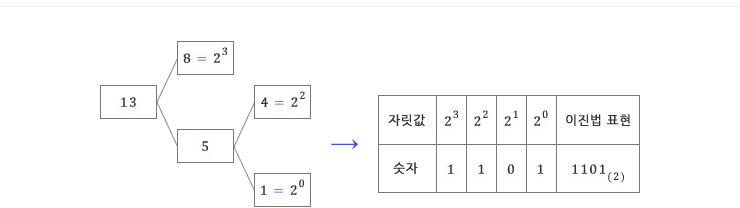
학창시절 십진법, 이진법에 대해서 공부하였다. 13을 이진법으로 나타내면 어떻게 표현될까? 그렇다, 13=1101(2)이다. 그런데, 궁금증을 가지게 하는 것이 한 가지 있었던 것 같다. 수학에서 수(number)라고 하면 보통 실수(real number)를 의미하는데, 이진법을 다룰 때는 항상 정수만 다루어 왔다는 점이다. 예를 들면 “13.8125 를 이진법으로 표현할 수 있을까?”라는 의문을 품을 수 있을 것 같다. 소수부분을 이진법이나 다른 n진법으로 표현하는 방법에 대해 알아보자. 이진법으로 나타내기 오랜 역사 동안 다양한 진법이 등장하였다. 지금은 대부분의 국가에서 십진법을 보편적으로 사용한다. 십진법이란 자리가 하나씩 옮겨감에 따라 자릿값이 1, 10, 102, 103, …, 10n으로 10배씩 커지는 방법으로 수를 나타내는 것이다. 예를 들어, 십진법으로 나타낸 수 1568은 1×103+5×102+6×10+8×100을 의미한다. 또한, 이진법이란 자리가 하나씩 옮겨감에 따라 자릿값이 1, 2, 22, 23, …, 2n으로 2배씩 커지는 방법으로 수를 나타내는 것을 말한다. 예를 들어, 이진법으로 나타낸 수 1101(2)은 1×23+1×22+0×2+1×20을 의미한다.

고대 마야인의 숫자가 그려진 돌. 고대 마야인은 20진법을 썼다. 가장 왼쪽 줄의 점과 막대 모양이 숫자이다. <출처: (cc) Madman2001 at Wikipedia.org>

중학교 교과서에서 중점적으로 다루는 것은 십진법으로 나타나 있는 수를 이진법으로 어떻게 나타내는가의 문제이다. 실제로 교과서에 ‘십진법을 이진법으로 바꾸는 방법’이 제시되어 있다. 만일 13을 이진법으로 나타낸다면, 아래와 같은 연속적인 나눗셈 방법에 의해서 1101(2)이다.

왜, 거꾸로 읽어 올라가는가? 앞의 ‘십진법을 이진법으로 바꾸는 방법’은 어떻게 나온 것일까? 그리고 나눗셈을 한 후 나머지로 나온 수를 왜 거꾸로 읽어 올라갈까? 이것에 대해 자세히 살펴보자. 이진법으로 표현된 수의 자릿값은 2의 거듭제곱 즉, 2n(n은 정수)의 형태이다. 따라서 십진법으로 표현된 수를 1, 2, 22, 23, …, 2n의 합으로 나타내면 된다. 예를 들어, 13을 2의 거듭제곱의 합으로 분할하여 보자.

‘십진법을 이진법으로 바꾸는 방법’이 옳다는 것은 위 그림과 표를 보면 이해가 갈 것이다. 이제 ‘십진법을 이진법으로 바꾸는 방법’을 분석해 보자.

위 그림 왼쪽의 ‘십진법을 이진법으로 바꾸는 방법’을 가로로 풀어 쓰면, 위 가운데 그림의 수식과 같다. 즉, 이진법으로 나타내기 위해 주어진 수를 2로 나누었을 때의 몫과 나머지를 순차적으로 구하는 과정을 제시한 것이다. 이러한 과정을 연속적으로 대입하여 하나의 수식으로 정리한 것이 위 그림 오른쪽이다. 따라서 ‘십진법을 이진법으로 바꾸는 방법’이 타당함을 확인할 수 있고, 거꾸로 올라가는 이유는 바로 이것 때문이다. 소수부분을 이진법으로 나타내기 십진법이나 이진법은 모두 수를 표현하는 한 방법이다. 따라서 십진법으로 나타나는 모든 수는 이진법으로 나타낼 수 있어야 한다. 그런데 소수부분이 있는 수는 어떻게 될까? 예를 들어 13.8125를 이진법으로 나타내는 경우를 생각해보자. 13.8152는 13+0.8125이며, 13은 이진법으로 1101(2)이다. 즉, 아래와 같다.

따라서, 소수점 이하 부분인 0.8125만 이진법으로 어떻게 나타낼 것인지 결정하면 된다. 다음과 같은 절차로 이 문제를 해결할 수 있다. 첫째, 자릿값을 결정한다. 십진법에서는 자릿값이 십의 거듭제곱인 10n이었다. 따라서 소수점 바로 앞의 자릿값이 100이며, 소수점 이하의 자릿값은 10-1, 10-2, 10-3, … 등이다. 이진법에도 이 원리는 동일하게 적용되므로, 소수점 이하의 자릿값은 2-1, 2-2, 2-3, … 등이 될 것이다. 둘째, 이진법으로 표현된 소수부분을 십진법으로 변환하는 방법을 생각해 보자. 앞에서 결정한 자릿값에 의해서 간단하게 고칠 수 있다. 이진법으로 표현된 1101.1101(2)을 예를 들어 보자.

마지막으로, 소수부분을 이진법으로 나타내는 방법을 알아보자. 이 방법은 기본적으로 정수부분에 대한 ‘십진법을 이진법으로 바꾸는 방법’과 본질적으로 동일하다는 것을 기억하자. 예를 들어 보자. 위에서 13.8125가 1101.1101(2)임을 알았으니, 0.8125를 이진법으로 고치면 0.1101(2)가 되어야 할 것이다. 이를 아래 그림을 통해 확인해 보자.

0.8125를 2의 거듭제곱의 역수로 분할하면 위 그림 왼쪽과 같고, 이를 정리하여 표로 나타내면 위 그림 오른쪽과 같다. 따라서 0.8125는 0.1101(2)임을 알 수 있다. 그런데 이와 같은 방법은 원칙적으로 적용이 가능하긴 하나, 쉽고 빨리 할 수 있는 방법은 아니다. 그렇다면, 십진법의 정수부분을 ‘이진법으로 바꾸는 방법’ 에서처럼, 십진법의 소수부분을 이진법으로 간단하게 바꿀 수 있는 방법은 어떻게 될지 생각해보자. 기본적으로 정수부분과 소수부분은 똑같은 원리가 적용된다는 점이다. 단지 정수부분의 자릿값은 2의 거듭제곱으로 증가하지만, 소수부분의 자릿값은 2의 거듭제곱의 역수로 감소한다는 차이가 있다. 따라서 2가 아니라 '1/2'을 얼마만큼 가지고 있는지 계산과정을 통해 찾아야 한다.

십진법 0.8125에서 '1/2'을 얼마만큼 가지고 있는지 찾는 과정은 위 그림 왼쪽에 제시되어 있다. 이진법으로 나타내는 것이 목적이므로 주어진 수에서 2-1을 순차적으로 뽑아내면 될 것이다. 이러한 과정을 연속적으로 대입하여 하나의 수식으로 정리한 것이 위 그림 오른쪽이다. 이를 통해 소수부분 0.8125를 이진법으로 나타낼 수 있음을 재확인할 수 있다. 이제 위의 왼쪽 그림을 이용하여 ‘소수부분을 이진법으로 간단하게 바꾸는 방법’을 제시하면 아래 그림과 같다.

소수부분 0.8125로부터 '1/2'을 뽑아낸 식에서 양변에 2를 곱하면, 소수부분에 2를 곱한 다음 정수부분과 소수부분을 분리한 것과 동일한 결과를 얻는다. 따라서 위 그림 오른쪽과 같이 소수부분에 2를 곱하는 과정을 연속적으로 반복한 것과 같은 결과를 얻는다. 이와 같은 방법으로 십진법으로 표현된 소수부분을 이진법으로 나타낼 수 있다. 결론적으로, ‘소수부분을 이진법으로 간단하게 바꾸는 방법’은 주어진 십진법의 소수부분에 2를 연속적으로 곱하고, 곱한 결과의 정수부분의 값만을 이진법의 각 자릿값의 수로 취하는 것이다. 소수부분을 다양한 진법으로 나타내기 이제 정수부분뿐 아니라 소수부분도 간단한 방법으로 이진법으로 바꿀 수 있음을 알게 되었다. 그렇다면, 소수부분을 이진법 이외의 다른 진법으로도 바꿀 수 있을까? 앞에서 구한 방법을 이용하여 0.8125를 5진법과 4진법으로 바꾸어 보자. 먼저 0.8125를 5진법으로 나타내는 방법을 알아보자. 십진법을 이진법으로 바꾸기 위해서는 소수부분에 2를 연속적으로 곱하였다. 따라서 5진법으로 바꾸기 위해서는 2대신에 5를 연속적으로 곱하면 될 것 같다. 0.8125를 5진법으로 바꾸는 방법은 아래 그림과 같다.

위 그림에서 5를 곱하는 과정을 네 번 반복하면 처음과 동일한 0.8125가 나타난다. 이는 순환마디를 4, 0, 1, 2로 가지는 순환소수가 됨을 의미한다. 따라서 다음과 같다.

다음으로 0.8125를 4진법으로 나타내는 방법을 알아보자. 십진법을 5진법으로 바꾸기 위해서는 소수부분에 5를 연속적으로 곱하였다. 따라서 4진법으로 바꾸기 위해서는 5대신에 4를 연속적으로 곱하면 될 것 같다. 0.8125를 4진법으로 바꾸는 방법은 아래 그림과 같다.

위 그림에서 4를 곱하는 과정을 두 번 반복하면 더 이상 계산할 필요가 없는 1.0000이 된다. 따라서 0.8125를 4진법으로 나타내면 다음과 같다.

도전해 볼 문제 0.8125를 분수로 나타내면 ’13/16’으로 분명히 유한소수이다. 그런데, 0.8125를 5진법으로 나타내면 순환소수가 되었고, 4진법으로 나타내면 소수 둘째 자리까지만 나타난다. 왜 이러한 현상이 일어나는지 생각해 보자.

글 서보억 / 대구가톨릭대학교 수학교육과 교수

한국교원대학교 수학교육과를 졸업하고, 한국교원대 대학원 수학교육학 석사, 국립경상대학교 대학원에서 수학교육학 박사학위를 받았다. 중등학교 수학교사, 한국교육과정평가원 전임연구원을 지냈으며, 저서로는 ‘3대 작도 문제 해결을 위한 곡선과 기구’ 등이 있다.